Question: How far do farts travel?
Short answer: About 10 ft.
Long answer: The movement of fart gas is well-characterized by the Diffusion Equation, which characterizes the spread of particles through a medium, in space and time. Here is a simplified version of the equation:
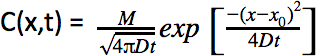
The left-hand side of the equation describes the concentration of fart smell at any distance x from the source x0 of the fart, and at any time t. Because this equation provides a good fit to our high-resolution data, we can infer the behavior of each fart from its best-fitting parameters. The parameters of interest here are the mass (per unit cross-sectional area) of fart gas M and the diffusivity coefficient D, which together tell us how smelly the fart was and how quickly it diffused.
Now the Diffusion Equation takes the form of a Gaussian function over space, with a width that varies over time. And since a Gaussian never actually goes to zero, it follows that farts never actually disappear. They just continue to spread, gradually slowing down for all eternity. Thus one answer to our question is that the distance traveled by farts is infinite, but this is not a very useful answer. In fact, as they spread further, the finite amount of smelliness is distributed over a larger volume, so that they eventually become undetectable to the human nose.
The threshold for detecting the chemical compounds that give farts their smell varies from individual to individual, but typically tends to be around 0.1 ppm. So we can rephrase our question: At what point does the VOC concentration of a typical fart fall below 0.1 ppm? We showed in a previous post that farts actually diffuse very slowly, so that it often takes more than a minute for the smell to reach the bottom of our collection tube, which has a length of 12”. Moreover, the diffusion slows with time. Using the equation above, we can calculate the timing of fart smells at larger distances from the source. Here are the results for an average fart:

The different lines show the time-course of fart stink at different distances, and the dashed line shows the olfactory threshold of 0.1 ppm. Of note here is the purple line, which corresponds to a distance of 120” or 10 ft. (or about 3 meters) from the source of the emission. This is the last distance at which the VOC levels reach 0.1 ppm, and it takes 17 hours for that to happen. Beyond that distance, the fart continues to spread, but would never be detectable on its own. Of course, multiple farts in the same space would presumably summate, so that the odor would be detectable at larger and larger distances. And as pointed out previously, the main factor determining the dispersion of smell is likely to be the movement of air in the environment. The point is that, undisturbed, fart smell moves very slowly.
These findings suggest that the average fart, which originates with a VOC level of 42.8 ppm, will gradually spread over a radius of about 10 ft, after which it effectively disappears from human perception. But what about farts that are more or less smelly than the average? It turns out that the relationship between smell, time and distance can be calculated analytically from the Diffusion equation. The trick is just to calculate the time point at which the VOC level is maximum at a given distance. This can be done by taking the temporal derivative of the diffusion equation and setting it to zero, which gives the time of peak stink for a given distance x:
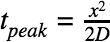
Substituting this back into the main equation yields this remarkably simple result, which relates the peak concentration to the initial mass deposited by the fart:
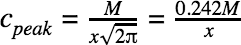
Therefore, the olfactory frontier of a fart, where cpeak = 0.1 ppm, occurs at distance x = kM, where k = 2.42. We refer to k as the flatological constant. From this result, we can conclude that the smelliest fart we have recorded to date, which clocked in at M = 722.9, would have traveled 145.8 ft. or about 44 meters.
